GEOMETRÍA ANALÍTICA EN EL PLANO
La geometría analítica es la que permite representar figuras geométricas mediante fórmulas del tipo f(x, y) = 0, donde f representa una función u otro tipo de expresión matemática.
En particular, las rectas pueden expresarse como ecuaciones polinómicas de primer grado y las circunferencias y el resto de cónicas como ecuaciones polinómicas de segundo grado.
La geometría analítica se desenvuelve en el llamado Plano cartesiano, para representar puntos en R² se lo hace de la siguiente forma:
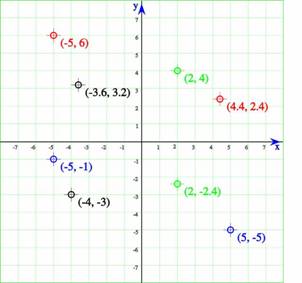
F(x,y) = 0 -------> Función implícita de dos variables.
i) y= f(x); donde la "y" es la variable dependiente y "x" es la variable independiente.
ii) x=g(y); donde la "x" es la variable dependiente y "y" es la variable independiente.
Fuente: www.profesorenlinea.cl
GEOMETRÍA ANALÍTICA EN EL ESPACIO
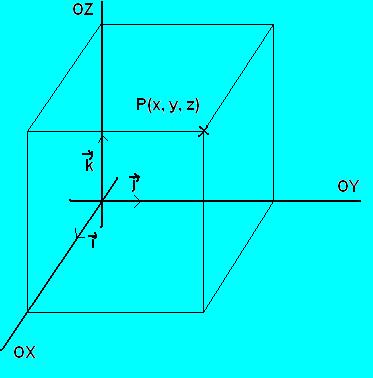
Consideremos tres rectas “x”, “y”, “z”, que son mutuamente perpendiculares y se intersecan en un mismo punto “O“. Éste punto se denominará origen de coordenadas y divide a cada eje en dos semiejes (positivo y negativo). Para cada punto “M” del espacio podemos encontrar las correspondientes coordenadas “P“, “Q“, “R“, de la siguiente forma.
El punto “P” es la intersección del eje “OX” con un eje paralelo al plano “yz” que pasa por “M“. De modo análogo se obtienen los puntos “Q” y “R” como resultado de la proyección del punto “M” en sus respectivos ejes coordenados.
La longitud de los segmentos es:
- OP = x.
- OQ = y.
- OR = z.
, de modo que a cada punto del espacio le asignaremos la terna ordenada de números (x, y, z).
Denotaremos por “i“, “j“, “k“, a los vectores unitarios coordenados cuya dirección y sentido es el positivo de estos ejes. Dado un punto arbitrario “M“, se cumple que su vector de posición satisface
- OM = OP + OQ + OR.
En términos de los vectores unitarios:
- OM = x i + y j + z k.
Siendo siempre:
- x = OM i.
- y = OM j.
- z = OM k.
La base (i, j, k) del espacio tridimensional es una base ortonormal, ya que todos sus vectores son unitarios y ortogonales dos a dos. Existe correspondencia biunívoca (única) entre cada punto “M” del espacio y el conjunto de las coordenadas cartesianas rectangulares (x, y, z).
Fuente: www.estudiarfisica.com
LA RECTA EN EL ESPACIO
La ecuación de la recta se puede encontrar mediante los datos que nos presente el ejercicio.
Existen dos casos:
1°Caso: Cuando se conoce un punto y un vector directriz.
Existen dos casos:
1°Caso: Cuando se conoce un punto y un vector directriz.

Ecuación Vectorial de la Recta
Ecuaciones Paramétricas de la Recta
Ecuaciones Canónicas de la Recta
2°Caso: Cuando se conoce dos puntos de la recta.

Ecuación Vectorial de la Recta
r→=r1−→+t(r2−→−r1−→)
Ecuaciones Paramétricas de la Recta
Ecuaciones Canónicas de la Recta
Distancia de un punto a una recta

La distancia de un punto a una recta es la longitud del segmento perpendicular a la recta, trazada desde el punto.


Distancia entre dos rectas
Datos:
Distancia:
Fuente: www.lanubeartistica.es
EL PLANO EN R³

Ecuaciones segmentarias del plano

Ecuación normal del plano
xcosα+ycosβ+zcosγ −ρ=0
Factor normalizante

- La desviación es (+) cuando el punto M y el origen de coordenadas están en lados opuestos del plano.
- La desviación es (-) cuando el punto M y el origen de coordenadas están del mismo lado del plano.
Distancia entre un punto y un plano
Fuente:
Plano determinado por tres puntos
Se realiza una operación de producto de vectores mixto (producto cruz y producto punto), tomando en cuenta que el Producto mixto de 3 vectores es igual a cero, entonces son coplanares.
Geométricamente esta operación es el volumen de un paralelepípedo donde sus aristas son los tres vectores involucrados.
(r→−r1−→)∙[(r2−→−r1−→)×(r3−→−r1−→)]=0
Geométricamente esta operación es el volumen de un paralelepípedo donde sus aristas son los tres vectores involucrados.
Recta Determinada Por 2 Planos
Donde (l,m,n) son componentes del vector director obtenido del producto cruz de los vectores normales del plano.
Una recta corta a los 3 planos coordenados en algún punto.
Ecuacion de un haz de planos
Haz de planos es un conjunto infinito de planos que pasan por una misma recta.
(A1x+B1y+C1z+D1)+λ(A2x+B2y+C2z+D2)=0
Ecuación vectorial de una superficie esférica

Fuente:
Superficies de segundo orden
Son aquellos que se representan por:
Ax2+By2+Cz2+Exy+Fxz+Hyz+Ix+Ky+Lz+M=0
Para realizar su análisis se sigue el siguiente procedimiento:
1.- Intersección con ejes coordenados.
2.- Intersección con los planos coordenados.
3.- Intersección con planos paralelos a los planos coordenados.
4.- trazar el bosquejo de la superficie.
Pasos Para Bosquejar Una Función.
1. Intersección con los ejes coordenados.

i ) Eje OX.
ii ) Eje OY.
iii ) Eje OZ.
2. Intersección con los planos coordenados.
i ) Plano YOX.
ii ) Plano ZOY.
iii ) Plano XOZ.
3. Paralelos con los planos coordenados.
i ) Paralelo al Plano YOX.
ii ) Paralelo al Plano ZOY.
iii ) Paralelo al Plano XOZ.







No hay comentarios:
Publicar un comentario