JUNIO

DERIVADA DIRECCIONAL.

DEFINICIÓN: La derivada direccional de f en (xo,yo) en la dirección de un vector unitario u= (a,b) es

si existe este limite

TEOREMA: Si f es una función diferenciable de x y de y, entonces f tiene una derivada direccional en la dirección de cualquier vector unitario u=(a,b) y 

GRADIENTE.

la derivada direccional se puede escribir como el producto punto de dos vectores:

El primer vector en este producto punto se presenta no solo al calcular las derivadas direccionales, sino también en muchos otros contextos.

DEFINICIÓN .- Si f es una función de dos variables x y y, entonces el gradiente de f es la funcion vectorial del gradiente definida por:

----> Realizamos dos ejemplo con la aplicación de las definiciones anteriormente revisadas. 

Casos Especiales.

fuente: www.locosfisica.com.ar

Máximos y mínimos relativos:

Una función z=f(x,y) tiene un máximo relativo (MR) en (a,b)

• Si: f(x,y)≤ f(a,b), cuando (x,y) está cerca de (a,b). El valor (a,b) recibe el nombre de máximo relativo de f(x,y).
• Si f(x,y)≥ f(a,b), cuando (x,y) está cerca de (a,b), entonces se dice que f(x,y) tiene un mínimo relativo (mR) en (a,b).

NOTA: Un punto de silla son puntos donde la f(x,y) presenta un MR con respecto a la una variable y un mR con respecto a la otra, a la vez.

Criterio de la segunda derivada:

Hallar las derivadas parciales de f con respecto a x y a y.

Igualar a cero las derivadas parciales encontradas anteriormente y encontrar los puntos críticos.

Hallar las derivadas parciales de segundo orden Fxx; Fxy; Fyy.

Determinar cada segunda derivada en los puntos críticos.

Formar el determinante Jessiano:

Aquí hay un video explicativo de Máximos y Mínimos:

Viernes, 12 de Junio del 2015

Máximos y Mínimos absolutos:

Toda función diferenciable en una región acotada y encerrada alcanza un valor máximo o mínimo, ó en un punto estacionario, ó en un punto de la frontera de la región.

Máximos y Mínimos Condicionados: Método de multiplicadores de Lagrange

Se denomina extremo condicionada de una función f(x,y), al valor máxim o mínimo de esta función alcanzadi con la condición (restricción) de que las variables independientes estén relacionadas con una ecuación de enlace: g(x,y)=0.

 Para hallar estos extremos condicionados debemos formar una FUNCIÓN DE LAGRANGE:

F(x,y,λ)=f(x,y)+λg(x,y)

INTEGRALES MÚLTIPLES.

Una integral múltiple se define como una integral definida de una función de dos variables o mas variables.

La integral múltiple tiene forma general de:

Para la resolución de dichas integrales se realiza el mismo procedimiento de una integral simple, pero varias veces hasta resolver cada operador, definido entre sus respectivos extremos.

Nota: Las integrales dobles representan el volumen bajo la superficie Z=f(x,y) y sobre la región R, siendo la región R parte del dominio de la función.

TIPOS DE REGIONES DE INTEGRACIÓN.

1. Integrales sobre regiones rectangulares 

En este caso, las integrales se dan sobre regiones acotadas por un rectángulo de vértices(a,b,c,d) en onde la integral toma la forma de: 

----->  Realizamos un ejercicios aplicando integrales en dicha región anteriormente estudiada

2.- Regiones mas generales.

Se presentan dos casos para integrar, en la cual se tiene en cuenta que parte de la región presenta punto fijos y cuales presenta puntos variables, y según eso se coloca el orden de los limites y el orden de realización de las  integrales.

----->  Realizamos un ejercicios aplicando integrales en dicha región anteriormente estudiada.

3.- Regiones generales.

Cuando tenemos una región que no sea rectangular, podemos transformarla en rectangular para hacer mas fácil la resolución de la integral múltiple.

Para esto, hacemos uso del Jacobiano de la transformación por la siguiente expresión:

Para facilitar el calculo de las integrales podemos usar transformaciones de coordenadas

1. Coordenadas rectangulares a coordenadas polares.
2. Coordenadas rectangulares a coordenadas cilíndricas.
3. Coordenadas rectangulares a coordenadas esféricas.

Fuente: wwww.vectorialmate.com

Centro de Masa

Centro de masa es el punto donde se concidera se concentra toda la masa de un cuerpo.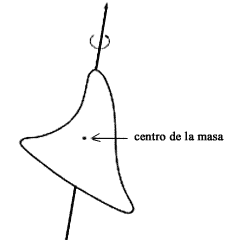

1. Caso Discreto

Se da cuando se tienen pocos puntos de referencia, por lo que se puede encontrar el centro de masa fácilmente: 

2. Si es un caso donde hay "n" masas:

En este caso, simplemente se generaliza la fórmula anterior, haciendo uso de la sumaroria.

3. Caso Continuo:

Cuando el numero de masas tiende al infinito.

1. Distribución de masa lineal

Cuando se tiene un cuerpo con una sola dimensión, se puede definir la siguiente igualdad

2. Distribución de masa superficial

Si se tiene un cuerpo de dos dimensiones, se utiliza un diferencial de área, y se define la siguiente igualdad:

3. Distribución de masa volumétrica

Cuando se tiene un cuerpo sólido de 3 dimesiones, para lo que se usa un diferencial de volumen, y se forma la igualdad:

Martes, 30 de Junio del 2015

Integrales de Línea

Son similares a las integrales simples solo que en vez de integrar en un intervalo [a,b] se integra en una curva C.

Estas Integrales resuelven problemas relacionados con el flujo de fluidos, fuerzas, electricidad y magnetismo 

Antes de comenzar a resolver es necesario parametrizar la función:

∫f(x,y)=∫tftof(x(t),y(t))x˙2+y˙2−−−−−−√dt

Cuando se tiene los puntos inicial y final del segmento rectilineo la representación vectorial para la parametrización es:

f(t)=xo+t(xf−x0)

Integrales de Linea en el espacio:

r(t)=x(t)i⃗ +y(t)j⃗ +z(t)z⃗ 

Entonces la integral de línea de f a lo largo de C, con respecto a la longitud de arco es:

∫f(x,y,z)=∫baf(x(t),y(t),z(t))(dxdt)2+(dydt)2+(dzdt)2−−−−−−−−−−−−−−−−−−−−−−√dt

Teorema Fundamental de las Integrales de Linea:

F=Pi⃗ +Qj⃗ +Rk⃗ 

∫∇f→dr⃗ =f(r→(b))−f(r→(a))

Debe ser un campo conservativo para eso cumple que:

∂P∂y=∂Q∂x;∂Q∂z=∂R∂y;∂P∂z=∂R∂x

Fuente: apuntes del cuaderno